Déplacement d'un joueur sur un graphe

Details: Written by Neamar; Category: Articles du blog; Created: 31 May 2010; Last Updated: 06 August 2013

Je commence aujourd'hui une petite série d'articles en préparation de mon nouveau jeu.
J'exposerai étape par étape les problèmes que j'ai rencontré et ma méthode de résolution.
Comme d'habitude, je ne garantis en rien qu'elle soit optimale (au contraire même ! ), et c'est tout juste si je garantis qu'elle fonctionne (mais j'ai tout de même fait assez de tests pour m'assurer de l'absence de bugs ! ).

Pendant que j'y suis aussi, coupons court aux malentendus : il ne s'agit pas de D-Graphe, même si les apparences sont trompeuses et que l'on va travailler avec un graphe.
Je donne le nom de code du jeu pour que les curieux tentent d'imaginer : mesdames et messieurs, préparez-vous à accueillir Eulris (normalement « eulrvis », mais c'est imprononçable sous nos latitudes) !

Dans cet article, nous ferons des maths (un peu), de l'algorithmie (plus), du debug (beaucoup) et de l'explication (encore plus).
Comme d'habitude, je choisis comme support AS3, c'est assez souple pour le réimplémenter en ce que vous voulez.

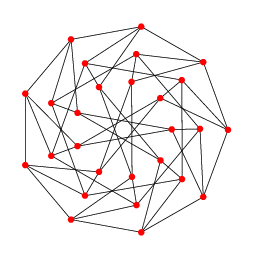
Graphe de Doyle, MathWorld

Problématique : trouver un moyen agréable, intuitif et fonctionnel pour laisser un utilisateur parcourir un graphe (une figure de jeu).

Justification de la problématique : imaginez un jeu qui implique de parcourir un graphe, celui-là par exemple :

Vous placez votre joueur sur le nœud (rouge) tout en haut, et vous voulez qu'il puisse « parcourir » le graphe pour arriver en bas.

Quelles solutions vous viennent à l'esprit ?

Au clavier :
- Utiliser les touches directionnelles. Mais comment représenter les 360° de latitude que peuvent prendre les arêtes sortant du point ? Ici il y en a 4, si on pose comme pré-requis que le nombre de « traits » sortants ne dépassera jamais 4, on peut attribuer à chacun une valeur directionnelle (haut, bas, gauche, droite) et laisser l'utilisateur faire. Les problèmes surviennent cependant rapidement : par exemple, si les quatre traits sont dirigés vers le bas, l'utilisateur aura du mal à établir une correspondance avec la touche haut. De même si les traits sortent en croix de St André (en diagonale) : l'extrémité partant en haut à gauche est-elle actionnée par l'appui vers gauche ? vers haut ? Bref, solution rejetée.
- Utiliser le pavé numérique, qui laisse 8 degrés de latitude. Mais on retombe sur les mêmes problèmes dans les cas limites !
- Placer un marqueur sur une arête (par exemple, d'angle le plus faible par rapport à l'horizontale) puis utiliser les touches gauche et droite pour sauter d'une arête. On perd ainsi la limite du nombre de traits sortants, mais on y perd aussi en ergonomie (il faut appuyer plusieurs fois sur une touche pour sélectionner la bonne arête). Gardons l'idée dans un coin de la tête.
À la souris :
- Au clic : on clique sur une arête pour effectuer un déplacement du point de départ vers le point relié par l'arête cliquée. L'idée est bonne, mais nécessite des bonnes capacités de maniement de souris pour être rapide, et la détection d'arêtes qui se chevauchent (proches du point de départ) est problématique.
- Pathfinding. L'utilisateur clique simplement sur un nœud, et l'ordinateur se charge de calculer le chemin le plus court. C'est assez aisé avec les technologies modernes (une liste chaînée fait des merveilles sur un algorithme A* brut)(encore que l'optimisation nécessite plus de réflexion, mais ici les nœuds sont peu nombreux ce qui limite le nombre de combinaisons à effectuer et donc la longueur du calcul). Le problème, c'est comment définir « chemin le plus court » ? Intuitivement, on pense à la longueur des arêtes, mais est-ce vraiment le résultat voulu ? Les cas sont nombreux ou la réponse est clairement non (encore une fois, cf. C-Graphe par exemple).

Personnellement, ce problème m'a bloqué pendant pas mal de temps (comprendre : ça a brisé mes élans de programmeur pour de nombreux mois ; j'avais des bons concepts mais j'étais incapable de les réaliser).
Et puis j'ai eu une idée très récemment, inspirée de l'algorithme de Jarvis (qui permet d'entourer un ensemble de points par une enveloppe).

Transplantée dans le monde réel, l'idée se résume en quelque mots. On prend une planche, on plante des clous à l'emplacement des nœuds. On accroche un bout de ficelle au clou de départ, puis on déroule la ficelle dans le plan de la planche.
Clarification (on ne clique pas, on déplace juste la souris ! ) :

Bon, comme d'habitude le graphisme est négligé (mais pour le jeu final préparez-vous à un graphisme du feu de Dieu, made in Licoti [qui travaille aussi sur la nouvelle version d'Omnilogie qui sortira sous peu, mais chut c'est un secret ! ])

Donc plutôt que d'avoir des phrases qui divergent grossièrement (« bite », celui qui comprend ce jeu de mot mal amené gagne un abonnement d'un an à mon blog), voyons les concepts derrière.

Et commençons par les choses qui fâchent, les mathématiques derrière. Histoire de ne pas perdre les lecteurs, je vais faire ça très court en vous présentant les deux seules fonctions techniques :

/**
 * Calcule l'angle entre la droite formée par les deux points et l'horizontale.
 * Valeur de retour comprise entre 0 et 2PI.
 * Note : l'ordre des paramètres est important !
 * Note : utilise la fonction atan2. Cf. http://fr.wikipedia.org/wiki/Atan2
 * @param	P1 le premier point
 * @param	P2 le second point
 * @return l'angle (P1P2,x)
 */
protected function getAngle(P1:Point, P2:Point):Number
{
	var Angle:Number = -Math.atan2(P2.y - P1.y, P2.x - P1.x);
	if (Angle < 0)
		Angle += 2 * Math.PI;

	return Angle;
}

/**
 * Distance pythagoréenne entre deux points.
 * @param	P1 le premier point
 * @param	P2 le deuxième point
 * @return la distance calculée avec le théorème de Pythagore.
 */
protected function getDistance(P1:Point, P2:Point):Number
{
	return Math.sqrt(Math.pow(P1.x - P2.x, 2) + Math.pow(P1.y - P2.y, 2));
}

Et nous voilà partis !
Plaçons le décor en examinant les acquis : on dispose d'une liste de points bien connus, de la position de la souris à tout instant, et de la liste des nœuds « accrochés ». J'utiliserai souvent le terme hook, hameçon, pour désigner ces points d'accroches.
Au démarrage, la liste ne contient que le premier nœud.

Ensuite, à chaque déplacement de souris il faut :

Calculer la distance D entre la souris et le dernier point d'accroche ;
Calculer l'angle θ_i (la direction en fait, puisqu'il est incohérent de parler d'angle entre deux points) entre la souris et le dernier point d'accroche, le _i symbolise le fait qu'il s'agit de θ à l'instant i ;
Récuperer tous les nœuds à une distance inférieure à d : ce sont des points d'accroches potentiels.
Pour chacun de ces nœuds :
- Calculer la direction φ dernier point d'accroche / nœud actuellement comparé
- Si la direction φ est comprise entre θ_i et θ_i-1 alors on ajoute le nœud courant aux points d'accroche.

Et voilà, c'est tout pour la base. Le problème, c'est qu'il y a pas mal de petits détails à régler :

D'abord, pour résoudre l'inégalité avec φ et θ, il faut disposer des angles du plus petit au plus grand (c'est incohérent de tester 5 < φ < 3 ! )
Ensuite, il y a le problème du « modulo 2π ». Imaginons que φ = 0, θ_i=0.1 et θ_i-1=2π-.1. On se rend bien compte qu'il y aura là un problème qu'il faudra gérer…

Tous les problèmes réglés, on obtient le code suivant. (Note : j'ai pré-calculé les angles φ pour accélérer les calculs)

//Déplacer le point représentant la souris
MousePos.x = mouseX;
MousePos.y = mouseY;

//Variables utiles aux calculs qui vont suivre
var DernierHook:Hook = getHook();
var AngleActuel:Number = getAngle(DernierHook.P, MousePos);
var AngleMin:Number = Math.min(AngleActuel, DernierAngle);
var AngleMax:Number = Math.max(AngleActuel, DernierAngle);
var Distance:Number = getDistance(DernierHook.P, MousePos);

if (AngleMax > 5 && AngleMin < 1)
{//On a tourné autour du cercle, il faut inverser les min et max et modifier l'angleMin pour ne pas avoir un saut de 2PI.
	var Swap:Number = AngleMax;
	AngleMax = AngleMin;
	AngleMin = Swap - 2 * Math.PI;
}

//Faut-il ajouter un hook ? Tester pour chacun des noeuds
for each(var Item:Position in Angles)
{
	//Si l'objet est différent du dernier hameçon (on ne s'accroche pas deux fois au même)
	//Que sa distance est inférieure à la distance de la souris
	//Et que l'angle est compris dans l'intervalle défini par les dernières mesures
	if (Item.P != DernierHook.P && Item.Distance < Distance && Item.Angle >= AngleMin && Item.Angle <= AngleMax)
	{//On a trouvé un hameçon !
		addHook(Item.P, (Item.Angle),0);
	}
}

//Enregistrer et dessiner.
DernierAngle = AngleActuel;
drawShape();

Et le résultat :

Mais là, on ne gère pas le décrochage d'un hameçon…
Pour cela, il va falloir enregistrer l'angle que fait la corde au moment de s'enrouler avec le nœud, mais aussi le sens dans lequel elle arrive (grossièrement, si elle arrive à gauche ou à droite). Arbitrairement, j'ai pris -1 pour le sens horaire et 1 pour le sens trigonométrique.

On ajoute donc la variable suivante dans le bloc de déclaration :

var Sens:int = (AngleActuel > DernierAngle)?1: -1;//Sens trigo // anti trigo

Il faut aussi penser à inverser le sens de rotation dans le petit if qui teste pour savoir si on a fait un tour (auquel cas on passera Sens = -Sens).

Et enfin, après la boucle pour l'ajout on ajoute une boucle pour la suppression :

//Faut-il enlever un hook ?
while(DernierHook.Sens != Sens && DernierHook.Angle >=AngleMin && DernierHook.Angle<=AngleMax)
{
	if(removeHook())
		DernierHook = getHook();
}

Et on obtient ainsi l'animation montrée plus haut.

Comme vous le voyez, en choisissant des primitives « intelligentes » (addHook(), removeHook(), getHook(), getAngle(), drawShape()) on peut se concentrer uniquement sur l'agorithmie et oublier les implémentations techniques.

Les curieux pourront télécharger le code, compilable même sans l'IDE d'Adobe. Comme d'habitude, il est relativement commenté et devrait être compréhensible.

Déplacement d'un joueur sur un graphe

Main Menu