Voilà une semaine paraissaient deux nouveaux jeux flash, qui venaient conclure une mini-série de jeux flash intitulée sans aucune originalité "Stacks".

 

Le principe est simple : une pile d'élements, on ne peut ramasser un objet que s'il n'est pas recouvert par un autre objet. Le but étant de récupérer le plus d'items en une minute...

En usant ce concept jusqu'à la corde, on obtient les trois jeux que je vais vous présenter...

• CoinStack : ramasser le plus de pièces possibles ! (ce jeu dispose d'une avance de deux mois sur les deux autres)
• Banknotestack : ramasser le plus de billets possibles !
• MoneyStack : ramasser le plus de monnaie possible !

Dans la suite de ce billet, nous examinerons un côté un peu plus technique des jeux...

 

 

On pourra légitimement se demander pourquoi CoinStack est sorti avant les autres, puisque tous les jeux sont similaires.

 

En fait, CoinStack est le plus simple à programmer : il suffit de tester la distance entre deux centres et de comparer avec les rayons des cercles. Il faut bien sûr optimiser tout cela pour ne pas se taper 500 comparaisons à chaque clic, mais rien de bien complexe : en s'aidant du z-order de la pièce cliquée, on peut facilement éviter de tester toutes celles en dessous. Et logiquement, si le joueur a compris la règle, il y a peu de pièces au dessus.

 

Pour BankNoteStack, le problème se complique. Car si la rotation de cercle ne pose pas de problèmes, la rotation de rectangles est une autre paire de manches.

 

Trouver si deux rectangles se chevauchent est un problème qui sort de la trivialité dès que les angles respectifs des rectangles sont différents de 0 degré. (on parle de collision de rectangles) En fait, il faut utiliser un théorème mathématique : le Separating Axis Theorem. Ceci nécessite de réaliser des projections selon les différents axes des rectangles, et de comparer les intersections selon chaque axe. Les techniques à maitriser ne sont pas extrêmement complexes (en fait, n'importe quel lycéen les maitrise : produits scalaire et vectoriels, normalisation de vecteurs), mais leur agencement  sort largement du programme de lycée.

Pour ceux qui seraient tentés par l'aventure, je ne peux que vous conseiller cet excellent tutoriel par les excellents créateurs de l'excellent jeu NGame.

 

Enfin, pour MoneyStack, il faut mélanger joyeusement tout cela (en considérant deux axes pour chaque cercle, orientés de la même manière que les axes du rectangle).

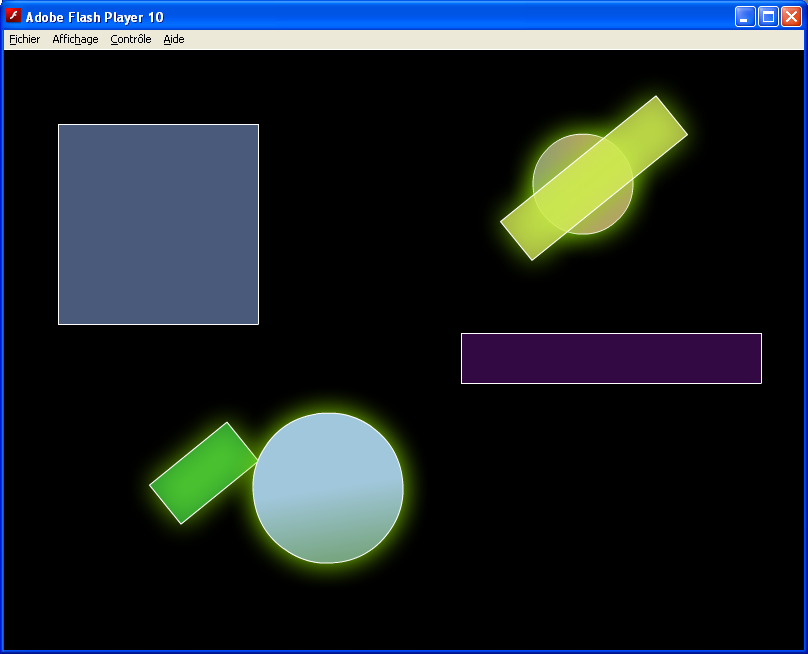
LA bonne nouvelle dans tout ça, c'est qu'une fois le moteur physique réalisé, il n'y a plus qu'à hériter des classes abstraites SATCircle et SATRectangle pour terminer le boulot.
Bon jeu à tous !